色情直播app

Next: 有向网络 Up: 网络上的静态几何量 Previous: 网络上的静态几何量

无向网络

目前已得到研究的典型无向网络包括：Internet网络，电影演员合作网络，科学家合作网络，人类性关系网络，蛋白质互作用网络，语言学网络，蛋白质折叠关系网络。

无向网络的基本几何量[1,2]有：度及其分布特征，度的相关性，集聚程度及其分布特征，最短距离及其分布特征，介数（Betweenness）及其分布特征，连通集团的规模分布。

一个顶点的度是指与此顶点连接的边的数量，即

d_v = $\displaystyle \sum_{{l\in E}}^{}$ $\displaystyle \delta^{{v}}_{{l}}$ ,

(1)

其中 $\delta^{{v}}_{{l}}$ 记号取值为1当边l包含顶点v，否则为零，即

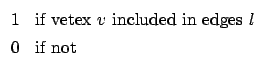$\displaystyle \delta^{{v}}_{{l}}$ = $\displaystyle \left\{\vphantom{ \begin{array}{ll} %array 表示矩阵的开始,ll说的?.. ...vetex $v$\ included in edges $l$} \\ 0 & \mbox{if not} \end{array} }\right.$ $\displaystyle \begin{array}{ll} %array 表示矩阵的开始,ll说的是两行,左对齐. 1 & \mbox{if vetex $v$\ included in edges $l$} \\ 0 & \mbox{if not} \end{array}$ ;

(2)

同时为了以后表述方便，我们定义其他两种类型的 $\delta$ 记号， $\delta^{{uv}}_{}$ 与 $\delta_{{lm}}^{}$ 分别表示顶点相邻与边相连；对于下一节中的有向网络， $\delta^{{uv}}_{}$ 与 $\delta^{{vu}}_{}$ 分别表示从u到v的有向联接和表示从v到u的有向联接， $\delta_{{lm}}^{}$ 推广为 $\delta_{{l\rightarrow m}}^{}$ , $\delta_{{l\leftarrow m}}^{}$ , $\delta_{{l\rightarrow\leftarrow m}}^{}$ $\delta_{{l\leftrightarrow m}}^{}$ ；对于加权网络，用记号 W_uv $\delta^{{uv}}_{}$ 代替 $\delta^{{uv}}_{}$ 就可以完整地描述，其中W_uv表示u、v之间联接的权重。

$\forall$ v $\in$ V我们都可以得到其度d_v。度值的分布特征是网络的重要几何性质。规则网络各顶点度值相同，因而符合 $\delta$ 分布，随机网络符合泊松分布（见3.1节），大量实际网络存在幂律形式的度分布[1,2]，称为无标度网络（Scale Free Networks），包括Internet网络[44,45]，电影与电视剧演员合作网络[18,32,46]，科学家合作网络[66,67]，人类性关系网络[47]，蛋白质互作用网络[48]，语言学网络[49]等，同时还存在高斯型，如蛋白质折叠网络[46]，和指数衰减型的概率分布，如电视剧演员合作网络[46]。

进一步的问题是，是否度分布可以完备地描述网络的特征呢？如果度分布与网络一一对应，我们就说度分布可以完整地描述网络，网络也只需要用度分布来描述。试想对于一给定的度分布，通过抽样，我们可以给对应网络的每一个顶点一个度值，保持度值的任意一种连接方式都构成一种网络。如果任意一种连接对应的其他几何量都一样，则我们认为实际上为同一网络。但是显然不能保证其他几何量也都一样。那么，保持度值不变的随机连接，即度与度之间没有相关性，是否可以成为大多数网络的代表呢？所以度分布之间的相关性是另一个重要的几何量。 Newman把它称为“匹配模式”[16]，意思是考察度值大的点倾向于和度值大的点连接，还是倾向于和度值小的点连接。具体的方法是，通过任意一条边都可以找到两个顶点，进而得到两个度值，这样通过所有的边我们就得到了两个序列，分析这两个序列的相关性即可。研究表明实际网络存在一定程度上的匹配模式，有的网络正向匹配，也有的网络反向匹配。但是，由于是无向网络，把哪一个顶点的度放入序列a，把哪一个顶点的度放入序列b是任意的，这一点对于相关性分析的影响并没有得到研究。实际网络的分析表明，不同的网络存在不同的匹配模式，有正相关也有负相关。

集聚程度的意义是网络集团化的程度，即考察连接在一起的集团各自的近邻之中有多少是共同的近邻。一种定义是对于每一个顶点v，找到其近邻集合N_v，记 n = $\left\vert\vphantom{N_v}\right.$ N_v $\left.\vphantom{N_v}\right\vert$ ，N_v中存在的边的数量为

M = 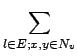$\displaystyle \sum_{{l\in E; x,y \in N_v}}^{}$ $\displaystyle \delta^{{x}}_{{l}}$ $\displaystyle \delta^{{y}}_{{l}}$ ,

(3)

则

C_v = $\displaystyle {\frac{{M}}{{C^{2}_{n}}}}$ .

(4)

于是我们可以得到所有顶点的集聚程度，它的统计分布是刻画网络的一个重要几何量，其平均值称为平均集聚程度C。

两点的最短路径l_ij定义为所有连通 $\left(\vphantom{i,j}\right.$ i, j $\left.\vphantom{i,j}\right)$ 的通路中，所经过的其他顶点最少的一条或几条路径。记 $\left(\vphantom{i,j}\right.$ i, j $\left.\vphantom{i,j}\right)$ 之间最短路径的集合为S_ij，相应的路径长度为 d_ij = $\left\vert\vphantom{l_{ij}}\right.$ l_ij $\left.\vphantom{l_{ij}}\right\vert$ 。如果 $\left(\vphantom{i,j}\right.$ i, j $\left.\vphantom{i,j}\right)$ 之间不存在通路，那么记d_ij = N。于是我们可以得到一个N x N的矩阵 $\left(\vphantom{d_{ij}}\right.$ d_ij $\left.\vphantom{d_{ij}}\right)_{{N\times N}}^{}$ 。其分布特征是一个重要的全局几何量，其平均值称为平均最短路径d。

另一个重要的全局几何量是介数（Betweenness）[17]。顶点u的介数含义为网络中所有的最短路径之中，经过u的数量。它反映了顶点u的影响力。记 $\left(\vphantom{i,j}\right.$ i, j $\left.\vphantom{i,j}\right)$ 之间最短路径的集合为S_ij，顶点u的介数定义为

B_u = 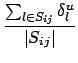$\displaystyle \sum_{{i,j}}^{}$ $\displaystyle {\frac{{\sum_{l\in S_{ij}}\delta^{u}_l}}{{\left\vert S_{ij}\right\vert}}}$ .

(5)

由此可以得到每一个顶点的介数B_v。实证研究表明，大量实际网络的介数分布也拥有共同的统计特征[17]。类似地，可以定义边的介数，Newman等人发现，边的介数可以用于分析顶点的聚类[24]。其基本思想是在包含不同集团的网络中所有最短路径经过次数最多的边，也就是介数最大的边，必然是联接两个集团之间的边。当然，建立在联接赋权基础上的 Hierarchical Clustering聚类算法也能给出网络上顶点的分类。

连通集团是指G的一个子图，在这个子图内，任意两点之间都存在通路。一个网络可能存在多个相互独立的连通集团。在渗流模型中，当系统处于临界状态时，连通集团的规模呈现出幂率分布。实证研究表明，对于大量的Scale-free 网络，连通集团的规模也存在幂率分布[1]。

关于无向网络的度分布还存在另外一种形式。计算近邻顶点的数目得到度值，然后把所有顶点的度值归一化后再把近邻顶点的度值相加得到顶点的二次度值，重复这一过程，直到得到稳定的度值[6]。这样得到的每一个顶点的度值实际上是邻接矩阵的最大本征值对应的本征向量，上述过程实际上就是矩阵本征值的最速下降法。但是这样的度分布具有的几何意义目前没有得到研究。

wwwwjs 2004-01-04